area boxes for distributive property Do your students struggle with multiplying large numbers? Help them learn multi-digit multiplication with strategies such as the area model, the box method, the partial products method, and the distributive property today! Click here to find .
$49.99
0 · distributive property multiplying methods
1 · distributive property multiplication
2 · distributive property geometry
3 · distributive property examples
4 · distributive property area model
5 · distribution property using area name
6 · area names for distributional properties
Design simplicity makes it a favorite for DIY'ers. Make this model your own. We used the engineering precision in our CAD systems to design in a range of configuration options. Tweak the plan from a matrix of door and window opening configurations, without the complexity and time of a custom design.
Distributive Property: Arrays and the Area Model . The Distributive Property. Definition: A number in a multiplication expression can be decomposed into two or more numbers. The distributive property can involve: multiplication over .

cnc milling machine pdf
This process of writing these products as a sum uses the distributive property. Use the distributive property to re-write each expression as a sum. You may want to draw a rectangle To use the distributive property, you need to break down the numbers into smaller parts. Once you have broken down the numbers, you can use the distributive property to multiply. To use the area model, draw a .value understanding using area models, partial products, and the properties of operations. Use models to make connections and develop the algorithm. STANDARD: NC.4.NBT.5
distributive property multiplying methods
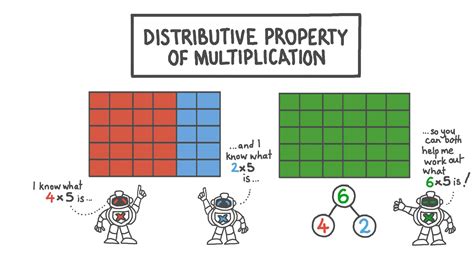
The distributive property of multiplication is used in all the methods we use to teach multi-digit multiplication. The area model, or box method, or window method for example is a .Do your students struggle with multiplying large numbers? Help them learn multi-digit multiplication with strategies such as the area model, the box method, the partial products method, and the distributive property today! Click here to find .
Anytime you see a number outside of a set of parentheses within an expression, you can use the distributive property to help you to simplify by writing an equivalent expression .Once the lesson begins, I remind students of the area model and how to make arrays. I start with a simple array, such as 3 x 6. After students have created the array, then I ask them to brainstorm all the ways that we can break up the six. Simplify \(8 \left(x − \dfrac{1}{4}\right)\) using the distributive property and explain each step. Explain how you can multiply 4(.97) without paper or a calculator by thinking of .97 as 6 − 0.03 and then using the . Instead of using the traditional way of expression called regrouping tens, it makes more sense to write it following the distributive property to a new learner, especially when larger numbers.
distributive property multiplication
distributive property geometry
Distributive Property: Arrays and the Area Model . The Distributive Property. Definition: A number in a multiplication expression can be decomposed into two or more numbers. The distributive property can involve: multiplication over addition (e.g., 6 x 47 = (6 x 40) + (6 x 7)) multiplication over subtraction (e.g. 4 x 98 = (4 x 100) – (4 x 2))

This process of writing these products as a sum uses the distributive property. Use the distributive property to re-write each expression as a sum. You may want to draw a rectangle
To use the distributive property, you need to break down the numbers into smaller parts. Once you have broken down the numbers, you can use the distributive property to multiply. To use the area model, draw a rectangle with the length and width representing the two factors.
value understanding using area models, partial products, and the properties of operations. Use models to make connections and develop the algorithm. STANDARD: NC.4.NBT.5 The distributive property of multiplication is used in all the methods we use to teach multi-digit multiplication. The area model, or box method, or window method for example is a great way to show the distributive property.Do your students struggle with multiplying large numbers? Help them learn multi-digit multiplication with strategies such as the area model, the box method, the partial products method, and the distributive property today! Click here to find out more. Anytime you see a number outside of a set of parentheses within an expression, you can use the distributive property to help you to simplify by writing an equivalent expression without parentheses. Let's look at an example.
Once the lesson begins, I remind students of the area model and how to make arrays. I start with a simple array, such as 3 x 6. After students have created the array, then I ask them to brainstorm all the ways that we can break up the six. Simplify \(8 \left(x − \dfrac{1}{4}\right)\) using the distributive property and explain each step. Explain how you can multiply 4(.97) without paper or a calculator by thinking of .97 as 6 − 0.03 and then using the distributive property.
Instead of using the traditional way of expression called regrouping tens, it makes more sense to write it following the distributive property to a new learner, especially when larger numbers.Distributive Property: Arrays and the Area Model . The Distributive Property. Definition: A number in a multiplication expression can be decomposed into two or more numbers. The distributive property can involve: multiplication over addition (e.g., 6 x 47 = (6 x 40) + (6 x 7)) multiplication over subtraction (e.g. 4 x 98 = (4 x 100) – (4 x 2))
This process of writing these products as a sum uses the distributive property. Use the distributive property to re-write each expression as a sum. You may want to draw a rectangle To use the distributive property, you need to break down the numbers into smaller parts. Once you have broken down the numbers, you can use the distributive property to multiply. To use the area model, draw a rectangle with the length and width representing the two factors.value understanding using area models, partial products, and the properties of operations. Use models to make connections and develop the algorithm. STANDARD: NC.4.NBT.5
The distributive property of multiplication is used in all the methods we use to teach multi-digit multiplication. The area model, or box method, or window method for example is a great way to show the distributive property.
distributive property examples
Do your students struggle with multiplying large numbers? Help them learn multi-digit multiplication with strategies such as the area model, the box method, the partial products method, and the distributive property today! Click here to find out more. Anytime you see a number outside of a set of parentheses within an expression, you can use the distributive property to help you to simplify by writing an equivalent expression without parentheses. Let's look at an example.Once the lesson begins, I remind students of the area model and how to make arrays. I start with a simple array, such as 3 x 6. After students have created the array, then I ask them to brainstorm all the ways that we can break up the six. Simplify \(8 \left(x − \dfrac{1}{4}\right)\) using the distributive property and explain each step. Explain how you can multiply 4(.97) without paper or a calculator by thinking of .97 as 6 − 0.03 and then using the distributive property.
distributive property area model
To curb that issue Purevolt has introduced Servo voltage stabilizer that provide stable output supply in case of unbalanced voltage. Especially applicable for CNC machines these Servo stabilizers corrects the input voltage variation and protects the sensitive circuit of the cnc machine.
area boxes for distributive property|distributive property geometry